Exercises

1.

Write a function called ``b-remove'' (for better remove), which takes a list and an element as arguments, and returns the original list with all occurrences of the element removed.

2.

Write a function called ``replace,'' which takes a list and two elements as arguments, and returns the original list with all instances of the first element replaced by the second element.

3.

Write a function which counts all of the atoms in a nested list.

4.

Write a function called ``insert,'' which takes a nested list and two atoms as arguments, and returns the original list in which the second atom has been inserted to the right of all occurrences of the first atom (if the first atom occurs in the list at all).

5.

A new mathematical, binary operator $ is defined as follows:

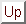
x $ y = x² + y

where x, y are integers. Extend the definition of ``evaluate'' presented earlier to include the operators $ and / (normal division).

6.

The Fibonacci series is defined as follows:

fib(n) = {fib(n-1) + fib(n-2) if n>1       }
         {1                   if n=0 or n=1}


    Implement a recursive function to calculate the nth fibonacci
    number.

7.
  Write a function called ``merge,'' which takes two number-lists
    of equal length.  It adds the corresponding members of each list
    and then returns the product of the resulting numbers.

For example, (merge '(1 2 3) '(2 2 2)) should return 60, since 
(1+2)*(2+2)*(3+2)=60.

8.
  Will the following piece of code always terminate?  Be careful to
    consider all possible cases.

          (defun mystery (n)
             (cond ((= n 0) 0)
                   (t (mystery (- n 1)))))